We use cookies to make your experience better. To comply with the new e-Privacy directive, we need to ask for your consent to set the cookies. Learn more.
Triangles in High School Geometry Part 1 Quick Reference Guide
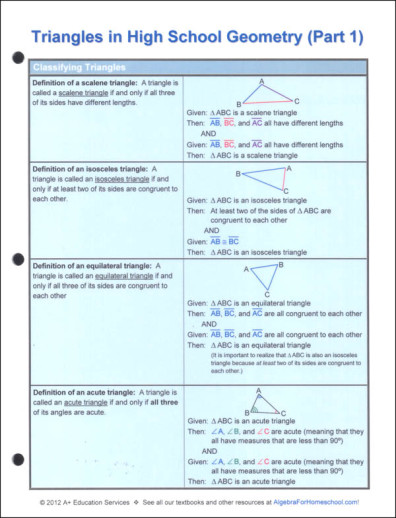
Our Triangles in High School Geometry (Part 1) Quick Reference Guide states all the definitions, postulates, and theorems found in a typical high school Geometry book that are associated with the following concepts:
* Classifying triangles
* The Sum of the Measures of the Angles in a Triangle Theorem and related concepts
* Congruent triangles
* Isosceles and equilateral triangles
* Inequalities in triangles
* The Pythagorean Theorem and related concepts
* Areas of triangles
Each definition, postulate, and theorem is accompanied by an example that shows exactly what the definition, postulate, or theorem tells you.
If you are looking for a different approach to Algebra with:
- Logically organized introduction of concepts
- Simple, clear explanations
- Student-directed instruction
- Non-intimidating text
- Work space in the text (or to photocopy and work)
- Thorough coverage of algebraic concepts without "extras" thrown in
- A discovery approach to learning
Then these texts may be just what you're looking for. The author has made clear choices to keep the course simple, understandable, self-directed, and easy to succeed at. Even the font sends a "you can do it" message. It's large, bold, crisp and clear with plenty of white space on each page. There are no side notes or rabbit trails here; everything is direct, on task, and pertinent to mastering Algebra. The result of this is a less overwhelming feel to the text. This approach would work well both for the student who is an independent learner and the student who doesn't particularly enjoy math (the "let's just get it done" type). Some children don't really care for the (exciting to me!) explanations and nuances of mathematics. They just need to learn it to get to college or go on to what they're really interested in. They need it like a tool to use; not like a painting to be studied and enjoyed. These are the children that will appreciate what Christy Walters (author) has done in this curricula. Her no-nonsense, straightforward explanations and examples will help both types of student focus on understanding how Algebra works and overcoming any reservations they may have about their ability to conquer the subject.
I appreciate that she has also incorporated self-discovery here; when a student makes their own connections, they understand and retain them. For example, she doesn't introduce the difference between two squares factoring method as a different way of factoring. She purposely made the decision to allow students to discover this unique relationship for themselves. The way she introduces factoring gives them the understanding and confidence they need to just tackle this unique problem like any other factorization problem. While there are techniques you can apply, many students do better if they intuit those independently through trial and error. This is especially true of children who don't do well remembering a bunch of rules and techniques. They are forever "lost" applying random techniques to a problem in an effort to find the "right" one, but without a clear sense of which one to apply! If I sound like a parent of a math-indifferent child, well, let's just say they're not all "chips off the old block"!
Mrs. Walters has, indeed, managed to keep it simple rather than mysterious, bewildering, and perplexing! It would be difficult for a child to be confused by the direct and understandable instruction. Moreover, she takes us through examples step by step and supplies many practice problems that grow gradually more complex. She concentrates on one skill at a time in progression from simple to complex. Her approach is stranded rather than spiral. Chapters are organized topically with a mixed review at the end of each. You will not revisit mastered concepts unless they are needed to solve more complex problems later. If you allow your child to "use" the text, they can write in it; she has left ample space to do so. Otherwise, you could photocopy the problem set pages and put them in a notebook. There are also note pages at the end of each chapter so the student can keep summary thoughts or points to remember together. Answers to odd-numbered problems are in the back of the text. Answers to all even problems (showing all solution steps) are contained in the Solution Guides. There is no separate teacher book or manual needed; the text contains all needed instruction. There are also no separate test books and keys. The Mixed Review problems at the end of each chapter are to be used for testing the understanding of all material in that chapter. The author has left her email address in the preface and welcomes all comments and/or suggestions.
The perfect component to round out this program is a complete set of tests. There is one test provided per chapter, and the tests vary from 2 to 4 pages in length. Tests in this packet correspond directly to chapter content, and beginning with chapter six they include a section of review problems on each test. Tests are printed on 8 ½ x 11 inch paper with plenty of space for students to show their work. The tests are not 3-hole punched, so the first thing I would do is punch them and put them in a binder.
This course is, indeed, a "fresh" approach. There is no "one size fits all" math curriculum, so if your child is having trouble with other traditional approaches, you might want to try this one on. Unlike some other programs out there, this one is comprehensive in coverage, not "dumbed down". While the methods are fresh, the course is serious in scope and is college preparatory. If you compare course content to Saxon, you will notice that it does not include topics that are normally taught in Geometry (or other branches of math - like box and whisker plots which are normally taught in Statistics). Read on for more details on the newly-released Geometry program!
Another uncluttered, fresh-looking math course from author Christy Walters. Again, I love that the book is addressed to the student, has plenty of workspace for problem-solving, and uses a no-nonsense approach. There is nothing "cute" here; just a direct, front-on approach to learning math. PLEASE READ THE DESCRIPTION for Algebra, if you are not familiar with the Algebra courses, as they function similarly. If you have used the Algebra I course, you will equally enjoy Geometry.
In the Geometry book, I like that she begins with a mini logic course (much like Jacobs). Instead of waiting until introducing geometric theorems to have the student begin doing proofs, she immediately introduces them in the context of what the student already knows (using algebraic principles). In this way, proofs are not a "new" thing used to prove just geometry theorems, but are familiar to the student as an extension and organization of logical thought. Although non-Euclidean geometry is an interesting topic in the Jacobs book, your math-reluctant student will appreciate not having to deal with such abstract concepts here. For a more complete idea of the scope and sequence of this course (and other geometry courses, for comparison), please visit our website to view the table of contents.
The thirteen chapters are broken into parts (lessons) with direct instruction followed by problems. Again, I like the self-discovery incorporated into the exercises as well as the short-answer questions, which require the student to put principles into words. The last part of each chapter is a mixed review including material from previous sections and chapters of the book. While the book is thick (730 pages before the answers to odd-problems section), the larger typeset font is easy on the eye and the less bulky text per page helps the instruction seem less intimidating and overwhelming. Since this book is intended for use between Algebra I and Algebra II, there is an Appendix devoted to a review of algebraic concepts. This is a great mini-refresher course and I am glad to see it all in one place at the end of the book rather than parceled out in the middle of the geometry course. I found the latter approach to be unnecessarily distracting in the Jacobs book.
Another notable feature of this series is the ability to work directly in the book or photocopy the student problem pages rather than recopying the problems and working on a separate sheet of paper. In the geometry course, this goes a step further in the inclusion of blank coordinate graphs on problems that require them. A companion DVD is also now included in the back of the book that includes extra help for chapters 2, 3, 12 and 13. The additional guidance on using a protractor, drawing 3-D shapes and perimeter, area and volume will be an asset to most students.
I really like this math series and would recommend it to any student, but particularly for children who seem confused by other math courses and for children who are working grade-levels ahead. It is a good text for the easily-distracted and math-phobic student as well - who needs to see things organized clearly and appreciates the less-cluttered feel of the text. If your child has had difficulty using other math programs, don't throw in the towel until you've tried "A Fresh Approach".
These comprehensive guides are packed with math information for your students. Written in an easy-to-understand fashion, these guides are uncluttered and more visually appealing than some of our other guides. They offer thorough coverage with clear examples and are 3-hole punched for easy storage. Each guide folds out to a generous 4 pages (front and back) of reference information and is laminated for durability. Written by the author of the Fresh Approach Math series, Christy Walters. ~ Donna
| Product Format: | Chart / Graph |
|---|---|
| Brand: | A+ Education Services |
| Grades: | 9-12 |
| Length in Inches: | 11 |
| Width in Inches: | 8.5 |
| Height in Inches: | 0.06 |
| Weight in Pounds: | 0.2 |